Interactions (IV)

class: center, middle, inverse, title-slide

# Interactions (IV)

---

## Last time...

- Factorial ANOVA

---

.pull-left[
The example data are from a simulated study in which 180 participants performed an eye-hand coordination task in which they were required to keep a mouse pointer on a red dot that moved in a circular motion.  
]
.pull-right[
![](images/dot.jpg)
]

The outcome was the time of the 10th failure. The experiment used a completely crossed, 3 x 3 factorial design. One factor was dot speed: .5, 1, or 1.5 revolutions per second.  The second factor was noise condition: no noise, controllable noise, and uncontrollable noise.  The design was balanced. 
---

### Marginal/cell means

<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;"> Noise </th>
   <th style="text-align:right;"> Slow </th>
   <th style="text-align:right;"> Medium </th>
   <th style="text-align:right;"> Fast </th>
   <th style="text-align:right;"> Marginal </th>
  </tr>
 </thead>
<tbody>
  <tr grouplength="3"><td colspan="5" style="border-bottom: 1px solid;"><strong></strong></td></tr>
<tr>
   <td style="text-align:left; padding-left: 2em;" indentlevel="1"> None </td>
   <td style="text-align:right;background-color: #EECACA !important;"> 630.72 </td>
   <td style="text-align:right;background-color: #B2D4EB !important;"> 525.29 </td>
   <td style="text-align:right;background-color: #FFFFC5 !important;"> 329.28 </td>
   <td style="text-align:right;color: white !important;background-color: grey !important;"> 495.10 </td>
  </tr>
  <tr>
   <td style="text-align:left; padding-left: 2em;" indentlevel="1"> Controllable </td>
   <td style="text-align:right;background-color: #EECACA !important;"> 576.67 </td>
   <td style="text-align:right;background-color: #B2D4EB !important;"> 492.72 </td>
   <td style="text-align:right;background-color: #FFFFC5 !important;"> 287.23 </td>
   <td style="text-align:right;color: white !important;background-color: grey !important;"> 452.21 </td>
  </tr>
  <tr>
   <td style="text-align:left; padding-left: 2em;" indentlevel="1"> Uncontrollable </td>
   <td style="text-align:right;background-color: #EECACA !important;"> 594.44 </td>
   <td style="text-align:right;background-color: #B2D4EB !important;"> 304.62 </td>
   <td style="text-align:right;background-color: #FFFFC5 !important;"> 268.16 </td>
   <td style="text-align:right;color: white !important;background-color: grey !important;"> 389.08 </td>
  </tr>
  <tr>
   <td style="text-align:left;background-color: white !important;"> Marginal </td>
   <td style="text-align:right;background-color: #EECACA !important;background-color: white !important;"> 600.61 </td>
   <td style="text-align:right;background-color: #B2D4EB !important;background-color: white !important;"> 440.88 </td>
   <td style="text-align:right;background-color: #FFFFC5 !important;background-color: white !important;"> 294.89 </td>
   <td style="text-align:right;color: white !important;background-color: grey !important;background-color: white !important;"> 445.46 </td>
  </tr>
</tbody>
</table>
---

## Running the analysis of variance

```r
fit = lm(Time ~ Speed*Noise, data = Data)
anova(fit)
```

```
## Analysis of Variance Table
## 
## Response: Time
##              Df  Sum Sq Mean Sq  F value    Pr(>F)    
## Speed         2 2805871 1402936 109.3975 < 2.2e-16 ***
## Noise         2  341315  170658  13.3075 4.252e-06 ***
## Speed:Noise   4  295720   73930   5.7649 0.0002241 ***
## Residuals   171 2192939   12824                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---

```r
lsr::etaSquared(fit)
```

```
##                 eta.sq eta.sq.part
## Speed       0.49786168   0.5613078
## Noise       0.06056150   0.1346807
## Speed:Noise 0.05247123   0.1188269
```

An effect size, `$\eta^2$`, provides a simple way of indexing effect magnitude for ANOVA designs, especially as they get more complex.

`$\eta^2$` represents the proportion of variance in Y explained by a single factor (or interaction of factors). It is identical in its calculation to `$R^2$`:

`$$\large \eta^2 = \frac{SS_{\text{effect}}}{SS_{\text{Y}}}$$`
---

```r
lsr::etaSquared(fit)
```

```
##                 eta.sq eta.sq.part
## Speed       0.49786168   0.5613078
## Noise       0.06056150   0.1346807
## Speed:Noise 0.05247123   0.1188269
```

In an experimental design, variance in Y is created, rather than observed, by manipulating participants. The ways in which an experimenter chooses to manipulate particiapnts can increase or decrease variance in Y, making it difficult to compare the effect of a single manipulation across studies with different designs.

Partial `$\eta^2$` is meant to aid interpretation by considering only the variance associated with an effect and random variablity, which is naturally occuring and not under the control of the experimenter.

`$$\large \text{Partial }\eta^2 = \frac{SS_{\text{effect}}}{SS_{\text{effect}} + SS_{\text{within}}}$$`

---

### Differences in means

In a factorial design, marginal means or cell means must be calculated in order to interpret main effects and the interaction, respectively. The confidence intervals around those means likewise are needed.

These means will be based on different sample sizes, which has an impact on the width of the confidence interval.

---

### Precision

If the homogeneity of variances assumption holds, a common estimate of score variability `$(MS_{within})$` underlies all of the confidence intervals.

`$$\large SE_{mean} = \sqrt{\frac{MS_{within}}{N}}$$`

`$$\large CI_{mean} = Mean \pm t_{df_{within}, \alpha = .05}\sqrt{\frac{MS_{within}}{N}}$$`

The sample size, `$N$`, depends on how many cases are aggregated to create the mean.

The `$MS_{within}$` is common to all calculations if homogeneity of variances is met.  The degrees of freedom for `$MS_{within}$` determine the value of `$t$` to use.
---

```r
anova(fit)
```

```r
library(emmeans)
(time_rg = ref_grid(fit))
```

```
## 'emmGrid' object with variables:
##     Speed = Slow, Medium, Fast
##     Noise = None, Controllable, Uncontrollable
```

```r
summary(time_rg)
```

```
##  Speed  Noise          prediction   SE  df
##  Slow   None                  631 25.3 171
##  Medium None                  525 25.3 171
##  Fast   None                  329 25.3 171
##  Slow   Controllable          577 25.3 171
##  Medium Controllable          493 25.3 171
##  Fast   Controllable          287 25.3 171
##  Slow   Uncontrollable        594 25.3 171
##  Medium Uncontrollable        305 25.3 171
##  Fast   Uncontrollable        268 25.3 171
```

---
The lsmeans( ) function produces marginal and cell means along with their confidence intervals. These are the marginal means for the Noise main effect.

```r
noise_lsm = emmeans::lsmeans(time_rg, "Noise")
```

```
## NOTE: Results may be misleading due to involvement in interactions
```

```r
noise_lsm
```

```
##  Noise          lsmean   SE  df lower.CL upper.CL
##  None              495 14.6 171      466      524
##  Controllable      452 14.6 171      423      481
##  Uncontrollable    389 14.6 171      360      418
## 
## Results are averaged over the levels of: Speed 
## Confidence level used: 0.95
```

---

```r
library(sjPlot)
noise_m = plot_model(fit, type = "emm", terms = c("Noise")) + 
  theme_sjplot(base_size = 20)
speed_m = plot_model(fit, type = "emm", terms = c("Speed")) + 
  theme_sjplot(base_size = 20)
library(ggpubr)
ggarrange(noise_m, speed_m, ncol = 2)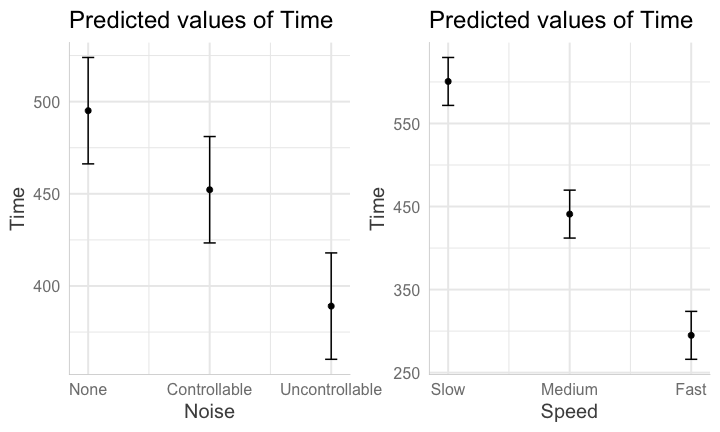
```

![](17-interactions_files/figure-html/unnamed-chunk-11-1.png)

---

```r
plot_model(fit, type = "pred", terms = c("Speed", "Noise")) + 
  theme_sjplot(base_size = 20) + theme(legend.position = "bottom")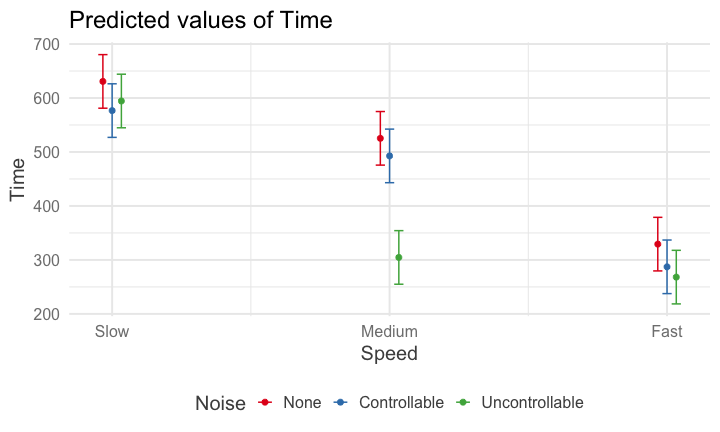
```

![](17-interactions_files/figure-html/unnamed-chunk-12-1.png)
---

### Precision

A reminder that comparing the confidence intervals for two means (overlap) is not the same as the confidence interval for the difference between two means.

$$
`\begin{aligned}
\large SE_{\text{mean}} &= \sqrt{\frac{MS_{within}}{N}}\\
\large SE_{\text{mean difference}} &= \sqrt{MS_{within}[\frac{1}{N_1}+\frac{1}{N_2}]} \\
\large SE_{\text{mean difference}} &= \sqrt{\frac{2MS_{within}}{N}} \\
\end{aligned}`
$$
---

### Cohen's D

`$\eta^2$` is useful for comparing the relative effect sizes of one factor to another. If you want to compare the differences between groups, Cohen's d is the more appropriate metric. Like in a t-test, you'll divide the differences in means by the pooled standard deviation. The pooled variance estimate is the `$MS_{error}$`

```r
fit = lm(Time ~ Speed*Noise, data = Data)
anova(fit)[,"Mean Sq"]
```

```
## [1] 1402935.71  170657.62   73929.93   12824.20
```

```r
MS_error = anova(fit)[,"Mean Sq"][4]
```

So to get the pooled standard deviation:

```r
pooled_sd = sqrt(MS_error)
```

---

### Cohen's D

```r
(noise_df = as.data.frame(noise_lsm))
```

```
##            Noise   lsmean       SE  df lower.CL upper.CL
## 1           None 495.0976 14.61974 171 466.2392 523.9560
## 2   Controllable 452.2079 14.61974 171 423.3495 481.0663
## 3 Uncontrollable 389.0759 14.61974 171 360.2175 417.9343
```

```r
(d_none_control = diff(noise_df[c(1,2), "lsmean"])/pooled_sd)
```

```
## [1] -0.3787367
```

---

### Follow-up comparisons

Interpretation of the main effects and interaction in a factorial design will usually require follow-up comparisons.  These need to be conducted at the level of the effect.

Interpretation of a main effect requires comparisons among the marginal means.

Interpretation of the interaction requires comparisons among the cell means.

The `emmeans` package makes these comparisons very easy to conduct.

---

```r
noise_lsm = emmeans::lsmeans(time_rg, "Noise")
```

```
## NOTE: Results may be misleading due to involvement in interactions
```

```r
pairs(noise_lsm, adjust = "holm")
```

```
##  contrast                      estimate   SE  df t.ratio p.value
##  None - Controllable               42.9 20.7 171 2.074   0.0395 
##  None - Uncontrollable            106.0 20.7 171 5.128   <.0001 
##  Controllable - Uncontrollable     63.1 20.7 171 3.053   0.0052 
## 
## Results are averaged over the levels of: Speed 
## P value adjustment: holm method for 3 tests
```

---

## Assumptions

You can check the assumptions of the factorial ANOVA in much the same way you check them for multiple regression; but given the categorical nature of the predictors, some assumptions are easier to check.

Homogeneity of variance, for example, can be tested using Levene's test, instead of examining a plot.

```r
library(car)
leveneTest(Time ~ Speed*Noise, data = Data)
```

```
## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)
## group   8  0.5879  0.787
##       171
```

---

## Unbalanced designs

If designs are balanced, then the main effects and interpretation effects are independent/orthogonal. In other words, knowing what condition a case is in on Variable 1 will not make it any easier to guess what condition they were part of in Variable 2.

However, if your design is unbalanced, the main effects and interaction effect are partly confounded.

```r
table(Data2$Level, Data2$Noise)
```

```
##       
##        Controllable Uncontrollable
##   Soft           10             30
##   Loud           20             20
```

---

### Sums of Squares

.pull-left[
In a Venn diagram, the overlap represents the variance shared by the variables. Now there is variance accounted for in the outcome (Time) that cannot be unambiguously attributed to just one of the predictors There are several options for handling the ambiguous regions.]
.pull-right[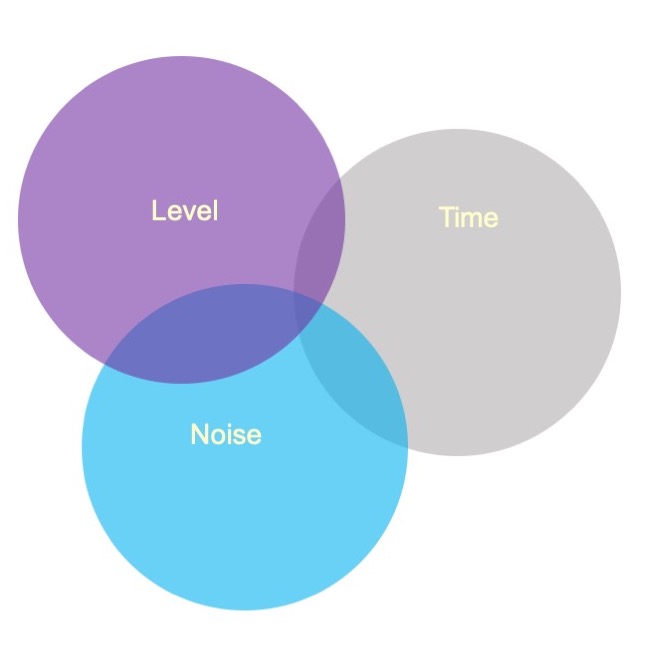
![](images/eta_sq_unbalanced.jpg)
]
---

### Sums of Squares (III)

.pull-left[
![](images/eta_sq_unbalanced_iii.jpg)]

.pull-right[
There are three basic ways that overlapping variance accounted for in the outcome can be handled.  These are known as Type I, Type II, and Type III sums of squares.

Type III sums of squares is the easiest to understand—the overlapping variance accounted for goes unclaimed by any variable.  Effects can only account for the unique variance that they share with the outcome.
]

---

### Sums of Squares (I)

.pull-left[
Type I sums of squares allocates the overlapping variance according to some priority rule.  All of the variance is claimed, but the rule needs to be justified well or else suspicions about p-hacking are likely.  The rule might be based on theory or causal priority or methodological argument.
]

.pull-right[
![](images/eta_sq_unbalanced_i.jpg)]

---

### Sums of Squares (I)
If a design is quite unbalanced, different orders of effects can produce quite different results.

```r
fit_1 = aov(Time ~ Noise + Level, data = Data2)
summary(fit_1)
```

```
##             Df  Sum Sq Mean Sq F value   Pr(>F)    
## Noise        1  579478  579478   41.78 8.44e-09 ***
## Level        1  722588  722588   52.10 3.20e-10 ***
## Residuals   77 1067848   13868                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

```r
lsr::etaSquared(fit_1, type = 1)
```

```
##          eta.sq eta.sq.part
## Noise 0.2445144   0.3517689
## Level 0.3049006   0.4035822
```

---
### Sums of Squares (I)
If a design is quite unbalanced, different orders of effects can produce quite different results.

```r
fit_1 = aov(Time ~ Level + Noise, data = Data2)
summary(fit_1)
```

```
##             Df  Sum Sq Mean Sq F value   Pr(>F)    
## Level        1 1035872 1035872   74.69 5.86e-13 ***
## Noise        1  266194  266194   19.20 3.68e-05 ***
## Residuals   77 1067848   13868                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

```r
lsr::etaSquared(fit_1, type = 1)
```

```
##          eta.sq eta.sq.part
## Level 0.4370927   0.4924002
## Noise 0.1123222   0.1995395
```

---
### Sums of Squares (II)

Type II sums of squares are the most commonly used but also a bit more complex to understand.

An approximately true description is that an effect is allocated the proportion of variance in the outcome that is unshared with effects at a similar or lower level.

A technically correct description is that a target effect is allocated the proportion of variance in the outcome that is unshared with other effects that do not contain the target.

---
### Sums of Squares (II)

In an A x B design, the A effect is the proportion of variance that is accounted for by A after removing the variance accounted for by B.

The A x B interaction is allocated the proportion of variance that is accounted for by A x B after removing the variance accounted for by A and B.

There is no convenient way to illustrate this in a Venn diagram.

---

### Sums of Squares

Let R(·) represent the residual sum of squares for a model, so for example R(A,B,AB) is
the residual sum of squares fitting the whole model, R(A) is the residual sum of squares 
fitting just the main effect of A, and R(1) is the residual sum of squares fitting just the
mean.

| Effect | Type I            | Type II           | Type III            |
|--------|-------------------|-------------------|---------------------|
| A      | R(1)-R(A)         | R(B)-R(A,B)       | R(B,A:B)-R(A,B,A:B) |
| B      | R(A)-R(A,B)       | R(A)-R(A,B)       | R(A,A:B)-R(A,B,A:B) |
| A:B    | R(A,B)-R(A,B,A:B) | R(A,B)-R(A,B,A:B) | R(A,B)-R(A,B,A:B)   |

---

### Sums of Squares

| Effect | Type I            | Type II           | Type III            |
|--------|-------------------|-------------------|---------------------|
| A      | SS(A)         | SS(A&#124;B)       | SS(A&#124;B,AB) |
| B      | SS(B&#124;A)       | SS(B&#124;A)       | SS(B&#124;A,AB) |
| A:B    | SS(AB&#124;A,B)    | SS(AB&#124;A,B)    | SS(AB&#124;A,B)   |

---

The `aov( )` function in R produces Type I sums of squares. The `Anova( )` function from the car package provides Type II and Type III sums of squares.

These work as expected provided the predictors are factors.

```r
Anova(fit, type = "II")
```

```
## Anova Table (Type II tests)
## 
## Response: Time
##              Sum Sq  Df  F value    Pr(>F)    
## Speed       2805871   2 109.3975 < 2.2e-16 ***
## Noise        341315   2  13.3075 4.252e-06 ***
## Speed:Noise  295720   4   5.7649 0.0002241 ***
## Residuals   2192939 171                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---

All of the between-subjects variance is accounted for by an effect in Type I sums of squares.  The sums of squares for each effect and the residual will equal the total sum of squares.

For Type II and Type III sums of squares, the sums of squares for effects and residual will be less than the total sum of squares. Some variance (in the form of SS) goes unclaimed.

The highest order effect (assuming standard ordering) has the same SS in all three models.

When a design is balanced, Type I, II, and III sums of squares are equivalent.

---

## Summary (and Regression)

Factorial ANOVA is the method by which we can examine whether two (or more) categorical IVs have joint effects on a continuous outcome of interest. Like all general linear models, factorial ANOVA is a specific case of multiple regression. However, we may choose to use an ANOVA framework for the sake of interpretability.

---

.pull-left[
#### Factorial ANOVA

Interaction tests whether there are differences in differences.

A main effect is the effect of one IV on the DV **ignoring the other variable(s)**.
]
.pull-right[
#### Regression

Interaction tests whether slope changes.

A conditional effect is the effect of IV on the DV **assuming all the other variables are 0**.
]

---

## Power

What is (statistical) power? How can we increase power?

The likelihood of finding an effect *if the effect actually exists.* Power gets larger as we:
* increase our sample size
* reduce (error) variance
* raise our Type I error rate
* study larger effects

---

![](17-interactions_files/figure-html/unnamed-chunk-23-1.png)

---

## Power in multiple regression (additive effects)

When calculating power for the omnibus test, use the expected multiple `$R^2$` value to calculate an effect size:

`$$\large f^2 = \frac{R^2}{1-R^2}$$`
---

### Omnibus power

```r
R2 = .10
(f = R2/(1-R2))
```

```
## [1] 0.1111111
```

```r
library(pwr)
pwr.f2.test(u = 3, # number of predictors in the model
            f2 = f, 
            sig.level = .05, #alpha
            power =.90) # desired power
```

```
## 
##      Multiple regression power calculation 
## 
##               u = 3
##               v = 127.5235
##              f2 = 0.1111111
##       sig.level = 0.05
##           power = 0.9
```

`v` is the denominator df of freedom, so the number of participants needed is v + p + 1.

---

### Coefficient power

To estimate power for a single coefficient, you need to consider (1) how much variance is accounted for by just the variable and (2) how much variance you'll account for in Y overall.

`$$\large f^2 = \frac{R^2_Y-R^2_{Y.X}}{1-R_Y^2}$$`
---
### Coefficient power

```r
R2 = .10
RX1 = .03
(f = (R2-RX1)/(1-R2))
```

```
## [1] 0.07777778
```

```r
pwr.f2.test(u = 3, # number of predictors in the model
            f2 = f, 
            sig.level = .05, #alpha
            power =.90) # desired power
```

```
## 
##      Multiple regression power calculation 
## 
##               u = 3
##               v = 182.1634
##              f2 = 0.07777778
##       sig.level = 0.05
##           power = 0.9
```

`v` is the denominator df of freedom, so the number of participants needed is v + p + 1.
---

## Effect sizes (interactions)

To start our discussion on powering interaction terms, we need to first consider the effect size of an interaction.

How big can we reasonably expect an interaction to be?

- Interactions are always partialled effects; that is, we examine the relationship between the product of variables X and Z only after we have controlled for X and controlled for Z. How does this affect the size of the relationship between XZ and Y?

???

The effect of XZ and Y will be made smaller as X or Z (or both) is related to the product -- the semi-partial correlation is always smaller than or equal to the zero-order correlation.

---

## McClelland and Judd (1993)

Is it more difficult to find interaction effects in experimental studies or observational studies?

What factors make it relatively easier to find interactions in experimental work?

---

### Factors influencing power in experimental studies

- No measurement error of IV 
    * don't have to guess what condition a participant is in
    * measurement error is exacerbated when two variables measured with error are multiplied by each other
    
- Experimentalists can force cross-over interactions; observational studies may be restricted to fan interactions
    * cross-over interactions are easier to detect than fan interactions

- Experimentalists can concentrate scores on extreme ends on both X and Z
    * in observational studies, data tends to cluster around the mean 
    * increases variability in both X and Z, and in XZ

- Experimentalists can also force orthognality in X and Z

???

Other things:

you can insure that you study the full range of X in an experiment, but you may have restricted range in an observational study

---

### McClelland and Judd's simulation

For the experiment simulations, we used 2 X 2 factorial designs, with values of X and Z equal to +1 and —1 and an equal number of observations at each of the four combinations of X and Z values.

```r
X = rep(c(-1,1), each = 50)
Z = rep(c(-1,1), times = 50)
table(X,Z)
```

```
##     Z
## X    -1  1
##   -1 25 25
##   1  25 25
```

---

### McClelland and Judd's simulation

For the field study simulations, we used values of X and Z that varied between the extreme values of +1 and —1. More specifically, in the field study simulations, values of X and Z were each sampled independently from a normal distribution with a mean of 0 and a standard deviation of 0.5. Values of X and Z were rounded to create equally spaced 9-point scales ranging from -1 to +1 because ranges in field studies are always finite and because ratings are often on scales with discrete intervals.

```r
X = rnorm(n = 100, mean = 0, sd = .5)
Z = rnorm(n = 100, mean = 0, sd = .5)
X = round(X/.2)*.2
Z = round(Z/.2)*.2

psych::describe(data.frame(X,Z), fast = T)
```

```
##   vars   n  mean   sd  min max range   se
## X    1 100  0.02 0.47 -1.2 1.0   2.2 0.05
## Z    2 100 -0.05 0.50 -1.2 1.2   2.4 0.05
```
---

For the simulations of both the field studies and the experiments, `$\beta_0 = 0, \beta_X=\beta_Z=\beta_{XZ} = 1.$` There were 100 observations, and errors for the model were sampled from the same normal distribution with a mean of 0 and a standard deviation of 4.

```r
Y = 0 + 1*X + 1*Z + 1*X*Z + rnorm(n = 100, mean = 0, sd = 4)
summary(lm(Y ~ X*Z))
```

```
## 
## Call:
## lm(formula = Y ~ X * Z)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -12.2691  -1.8418  -0.0396   2.6666   9.1478 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)   0.1573     0.4070   0.386    0.700
## X             0.7812     0.8712   0.897    0.372
## Z             0.6686     0.8108   0.825    0.412
## X:Z           0.9635     1.9267   0.500    0.618
## 
## Residual standard error: 4.043 on 96 degrees of freedom
## Multiple R-squared:  0.01752,	Adjusted R-squared:  -0.01318 
## F-statistic: 0.5706 on 3 and 96 DF,  p-value: 0.6357
```

---

From 100 simulations each, estimates of the model parameter `$\beta_{XZ}$` the moderator or interaction effect equaled 0.977 and 0.979 for the field studies and experiments, respectively.

```r
set.seed(0305)
```

.pull-left[

```r
# for experimental studies
sim = 100
ebeta_xz = numeric(length = 100)
et_xz = numeric(length = 100)
for(i in 1:sim){
  # simulate data
  X = rep(c(-1,1), each = 50)
  Z = rep(c(-1,1), times = 50)
 
  
   Y = 0 + 1*X + 1*Z + 1*X*Z + 
    rnorm(n = 100, mean = 0, sd = 4)
  #run model
  model = lm(Y ~ X*Z)
  coef = coef(summary(model))
  #extract coefficients
  beta = coef["X:Z", "Estimate"]
  t_val = coef["X:Z", "t value"]
  #save to vectors
  ebeta_xz[i] = beta
  et_xz[i] = t_val
}
```
]
.pull-right[

```r
# for observational studies

obeta_xz = numeric(length = 100)
ot_xz = numeric(length = 100)
for(i in 1:sim){
  # simulate data
  X = rnorm(n = 100, mean=0, sd = .5)
  Z = rnorm(n = 100, mean=0, sd = .5)
  X = round(X/.2)*.2
  Z = round(Z/.2)*.2
  Y = 0 + 1*X + 1*Z + 1*X*Z + 
    rnorm(n = 100, mean = 0, sd = 4)
  #run model
  model = lm(Y ~ X*Z)
  coef = coef(summary(model))
  #extract coefficients
  beta = coef["X:Z", "Estimate"]
  t_val = coef["X:Z", "t value"]
  #save to vectors
  obeta_xz[i] = beta
  ot_xz[i] = t_val
}
```
]
---

```r
mean(ebeta_xz)
```

```
## [1] 0.9440304
```

```r
mean(obeta_xz)
```

```
## [1] 1.175444
```

![](17-interactions_files/figure-html/unnamed-chunk-33-1.png)

---

```r
mean(et_xz)
```

```
## [1] 2.383435
```

```r
mean(ot_xz)
```

```
## [1] 0.7411209
```

![](17-interactions_files/figure-html/unnamed-chunk-35-1.png)

---

```r
cv = qt(p = .975, df = 100-3-1)
esig = et_xz > cv
sum(esig)
```

```
## [1] 66
```

```r
osig = ot_xz > cv
sum(osig)
```

```
## [1] 12
```

In our simulation, 66% of experimental studies were statistically significant, whereas only 12% of observational studies were significant. Remember, we built our simulation based on data where there really is an interaction effect (i.e., the null is false).

McClelland and Judd found that 74% of experimental studies and 9% of observational studies were significant.

---

### Efficiency

???
Efficiency = the ratio of the variance of XZ (controlling for X and Z) of a design to the best possible design (upper right corner). High efficiency is better; best efficiency is 1.

---

### Efficiency

.pull-left[
If the optimal design has N obserations, then to have the same standard error (i.e., the same power), any other design needs to have N*(1/efficency).

So a design with .06 efficency needs `$\frac{1}{.06} = 16.67$` times the sample size to detect the effect. 
]

.pull-right[
![](images/common.png)
]

This particular point has been ["rediscovered"](https://statmodeling.stat.columbia.edu/2018/03/15/need-16-times-sample-size-estimate-interaction-estimate-main-effect/) as recently as 2018:

* you need 16 times the sample size to detect an interaction as you need for a main effect of the same size.

???

This generalizes to higher-order interactions as well. If you have a three-way interaction, you need 16*16 (256 times the number of people).

---

## Observational studies: What NOT to do

Recode X and Z into more extreme values (e.g., median splits)
    * while this increases variance in X and Z, it also increases measurement error

Collect a random sample and then only perform analyses on the subsample with extreme values
    * reduces sample size and also generalizability
    
#### What can be done?
M&J suggest oversampling extremes and using weighted and unweighted samples

---

## Experimental studies: What NOT to do

Be mean to field researchers

Forget about lack of external validity and generalizability

Ignore power when comparing interaction between covariate and experimental predictors (ANCOVA or multiple regression with categorical and continuous predictors)